法线贴图的主要原理是改变贴图的法线从而改变物体的颜色变化，产生一种凹凸感，我们需要弄明白如何将法线进行改变

重要概念

  1. 法线贴图：由于需要对物体的法线进行改变，我们需要对改变的法线进行存储，贴图用RGB存储颜色，法线贴图用RGB存储法线方向
  2. 切线空间：切线空间主要用于法线贴图的坐标系确立，由于物体在世界坐标系是不断变化的，我们没法使用世界坐标系作为法线贴图的坐标系，需要建立一个可以确认物体某个点的法线是固定不变的坐标系，这样我们才能对法线做出正确的变换。我们将物体的法线（N)，顶点的切线(T)以及法线切线叉乘确认的副切线(B)作为形成的[T,B,N]矩阵作为切线空间的坐标系，而法线贴图的法线就是定义在这个坐标系下的
  3. 顶点切线、副切线的获取：三个顶点构成的平面和切线副切线的平面是共面的，如下图，而顶点坐标都是已知的，我们可以推倒出切线，副切线，Unity中会将切线信息存储在顶点中，副切线通过叉乘获得 具体推倒过程

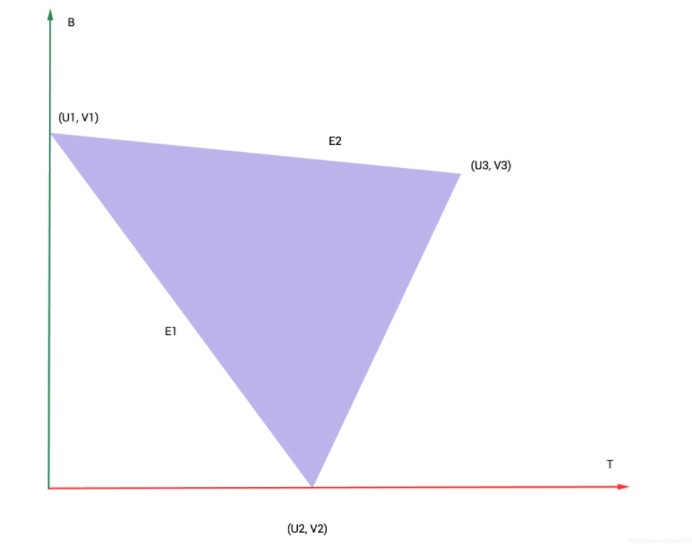
  1. 正交基与坐标系转换： TBN矩阵的每个向量都需要进行归一化形成正交基，正交基的特点是每个基向量都是单位向量且相互垂直，这样的矩阵有个好处是逆矩阵和转置矩阵是一致的。向量计算是要在同一个坐标系下进行的，需要进行坐标系转换，TBN矩阵是切线空间的基向量在世界空间的表示，世界空间的向量左乘TBN可以实现向量从世界空间转换到切线空间，切线空间左乘TBN的逆矩阵可以实现向量从切线空间转换到世界空间。如切线空间中向量是（1,1,0）左乘(T,B,N)后 = T + B为世界坐标系下的两个基向量相加

注意点

  1. 法线贴图的法线是通过RGB存储的范围在（0,1）的区间，是(normal + 1 / 2)获得的，在实际运用过程中我们需要将采样值进行*2 -1恢复（-1,1）的法线方向
  2. 副切线B是通过叉乘获取到的，但是在左右手坐标系下叉乘遵循不同定则，在左手坐标系 B = cross(N,T),右手坐标系 T = cross(T,N)
  3. 貌似是为了代码互通，Tangent是以float4存储的，在得到副切线后需要乘上Tangent.w，获得最后的副切线方向，由于是左手坐标系Unity中，Tangent.w固定为-1
  4. Unity中 half3x3 TBN = half3x3(T, B, N)默认为行向量
  5. 由于存在一个顶点被多个平面所共享导致向量和切线不能相互垂直，导致TBN不是正交基，造成偏移，需要进行进行施密特正交化将切线和法向量变为相互垂直

实现思路与关键代码

​ 有两种实现方式，一种是将向量计算转移到世界空间（或者模型空间），一种是都转移到切线空间，如果是第一种，我们将TBN传入片元着色器，对法线贴图的采样结果进行变换，如果是第二种，我们可以在顶点着色器就将光照进行变换传入片元着色器，这样就减少了很多矩阵运算。

以下为单平行光源仅计算漫反射情况的关键代码：

无法线贴图

1
2
3
4
5
fixed4 frag(v2f i) : SV_Target{    
    half colorDirectDiffuse = dot(normalize(-_DirDirect), normalize(i.worldNormal));
    half3 colorDirect = colorDirectDiffuse  * _ColorDirect * _IntentDirect;
    return tex2D(_MainTex, i.uv) * colorDirect;
}

第一种 转到世界空间

1
2
3
4
5
6
7
8
9
 fixed4 frag(v2f i) : SV_Target{
    fixed3 binormal = cross(i.worldNormal, i.worldTangent) * i.tw;
    //转置获得TBN逆矩阵
    fixed3x3 TBN = transpose(half3x3(normalize(i.worldTangent), normalize(binormal), normalize(i.worldNormal)));
    fixed3 norMap = tex2D(_NorTex, i.uv).rgb * 2 - 1;
    fixed colorDirectDiffuse = dot(normalize(-_DirDirect), normalize(mul(TBN,norMap)));
    fixed4 colorDirect = colorDirectDiffuse * _ColorDirect * _IntentDirect;
	return tex2D(_MainTex, i.uv) * colorDirect;
}

第二种 转到切线空间(推荐)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
v2f vert(a2v v) {
    v2f o;
    o.pos = UnityObjectToClipPos(v.vertex);
    o.uv = v.texcoord.xy;
    fixed3 worldNormal = normalize(UnityObjectToWorldNormal(v.normal));
    fixed3 worldTangent = normalize(UnityObjectToWorldDir(v.tangent));
    //正交化
    worldTangent = normalize(worldTangent - dot(worldNormal, worldTangent) * worldNormal);
    fixed3 binormal = cross(worldNormal, worldTangent) * v.tangent.w;
    fixed3x3 TBN = fixed3x3(worldTangent, binormal, worldNormal);
    o.dirDirectInTSpace = normalize(mul(TBN, -_DirDirect));
    return o;
}

fixed4 frag(v2f i) : SV_Target{
    fixed3 norMap = tex2D(_NorTex, i.uv).rgb * 2 - 1;
    fixed colorDirectDiffuse = dot(i.dirDirectInTSpace, normalize(norMap));
    fixed4 colorDirect = colorDirectDiffuse * _ColorDirect * _IntentDirect;
    return tex2D(_MainTex, i.uv) * colorDirect;
}

效果

左边为实现效果，中间为Unity中的BumpMap效果，右边为不带法线贴图的效果