顶点法线切线UV和三角面
参考文献:关于顶点的法线、切线、副切线 切线空间与UV坐标 为什么要有切线空间(Tangent Space)
我们知道Mesh(网格)决定了物体的形体结构,其中包含的数据也是渲染物体的基本数据来源,Mesh包含的数据主要是顶点数据和图元数据,这边的图元又可以是点、线、可三角面,或是是其他多边形,在Unity中图元一般为三角面。顶点数据包含了顶点位置、UV、顶点法线、切线等信息,三角面包含了构成三角面的顶点数据。
如下图所示,一个正方形有6个面,8个顶点,但是它有24份顶点数据,12个三角面。

那么为什么不是8份顶点数据呢,因为如果只有8份顶点数据,也就是每个顶点一个数据,那么一个顶点就只有一个法线,一个顶点法线被三个面共享的话。可以明显看到,正方形的顶点上的三个面的光照表现是截然不同的,也就是需要法线的突变,而一个顶点法线被三个面共享的话,这样三个面的法线数据会被插值,就会使一种平滑的光照表现,如下图,显然这种光照表现是不对的,因此至少需要24份顶点法线数据。此外,对于一个一个正方形的面,要自定义它的UV,至少需要4个顶点UV,因此,至少24份顶点UV数据。所以至少需要24份顶点数据。
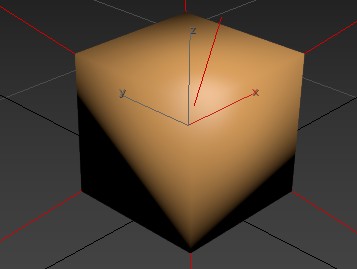
理论上12个三角面,每个三角面三份顶点数据,应该是需要36份数据的。但是由于在同一个面上的两个三角面的共享顶点的顶点数据是完全相等的,因此为了减少计算量,就把这些完全相等的数据舍去了,每个面减掉2份,一共减掉12份,最终剩下24份顶点数据。
根据我的测试可以得出以下结论:
- 如果模型有m个顶点,n个三角面,则顶点数据最少有m份,最多有n*3份。
- 顶点数据的数量,即Unity 里的 verts数,决定了进入顶点着色器的次数。
- 顶点的法线、切线、uv等信息的不同都会导致顶点数据的增加。
- 对于通过顶点所在三角面算出的顶点法线、切线数据,有可能会出现不同,但是最终形成几份顶点数据是不一定的。比如,在曲面上,顶点通过它的三角面算出了不同的法线,但最终会被通过一些平均算法,算出一个法线,形成一份顶点数据,但是如果是在曲面和其他面的边缘位置,则会将曲面上的片元算出一个平均法线,其他面再算出一个法线,形成两份顶点数据。
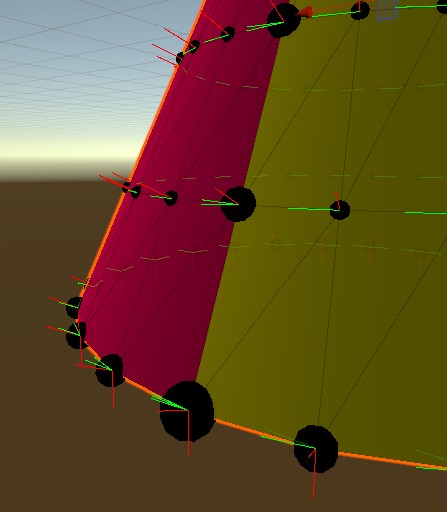
对于第四点,需要举个例子进行特别说明,如下图的梯台,其中小黑球代表1份顶点数据,中黑球代表2份顶点数据,大黑球代表3份顶点数据,红线表示法线,绿线表示切线,该梯台一共有6 * 24 个顶点(6个圈,每个24个顶点),在曲面的上的顶点基本都是1份顶点数据,上下边缘为了表现边缘效果,需要两个不同的顶点法线,因此增加了24 * 2份顶点数据。此外,在曲面的一条线上,UV值发生了1->0的突变,因此1个顶点需要有两份顶点数据,又增加了6份顶点数据,并且这6份顶点数据所在的顶点在算切线的时候本身是有两个的切线的,其他曲面上的点在曲面上和法线一样进行了平均,但这边反正都因为UV分成两个了,干脆切线也就分成两份存了,反正不会多生成顶点数据。
结合这个例子,可以看出,对于顶点法线和切线不同的时候,顶点数据到底该划分成多少份是有一定灵活性的。Unity一般都会在满足效果要求下,尽可能降低顶点数据的数量,来提高渲染效率。
接下来说明下顶点数据的切线,法线以及副切线的计算规则
初始,我们有的数据是每份顶点数据的顶点位置、顶点UV值,以及每个三角面的三份顶点数据
第一步,根据三个顶点位置信息和平面方程,我们可以算出三角面面法线,代码如下:
public Vector3 Cal_Normal(Vector3 v1, Vector3 v2, Vector3 v3)
{
//平面方程: na * (x – n1) + nb * (y – n2) + nc * (z – n3) = 0 ;
float na = (v2.y - v1.y) * (v3.z - v1.z) - (v2.z - v1.z) * (v3.y - v1.y);
float nb = (v2.z - v1.z) * (v3.x - v1.x) - (v2.x - v1.x) * (v3.z - v1.z);
float nc = (v2.x - v1.x) * (v3.y - v1.y) - (v2.y - v1.y) * (v3.x - v1.x);
return Vector3.Normalize(new Vector3(na, nb, nc));
}
第二步,根据三个顶点位置信息和UV信息,我们可以算出三角面的切线,
切线的数学定义实际是三角形模型空间坐标对于U的偏导数

其公式推倒过程如下

代码如下:
public Vector4 Cal_Tangent(Vector3 v1, Vector3 v2, Vector3 v3, Vector2 uv1, Vector2 uv2, Vector2 uv3)
{
Vector3 e1 = v2 - v1;
Vector3 e2 = v3 - v1;
Vector2 uvo1 = uv2 - uv1;
Vector2 uvo2 = uv3 - uv1;
float hanglieshi = 1f / (uvo1.x * uvo2.y - uvo2.x * uvo1.y);
Vector3 juzhencheng = new Vector3(uvo2.y * e1.x + -1f * uvo1.y * e2.x, uvo2.y * e1.y + -1f * uvo1.y * e2.y, uvo2.y * e1.z + -1f * uvo1.y * e2.z);
Vector3 t = Vector3.Normalize(hanglieshi * juzhencheng);
//-1代表切线方向
return new Vector4(t.x, t.y, t.z, -1f);
}
第三步,顶点根据它所在三角面的面法线和切线得出顶点法线和切线,这边算法应该有多种,这边都采用直接相加标准化
代码如下:
public Vector3 Cal_Normal(List<MyFace> faceList)
{
Vector3 normal = new Vector3(0, 0, 0);
foreach(MyFace face in faceList)
{
if(face.ContainVert(this)) normal += face.normal;
}
return Vector3.Normalize(normal);
}
public Vector4 Cal_Tangent(List<MyFace> faceList)
{
Vector3 tangent = new Vector3(0, 0, 0);
foreach (MyFace face in faceList)
{
if (face.ContainVert(this)) tangent += new Vector3(face.tangent.x,face.tangent.y,face.tangent.z);
}
tangent = Vector3.Normalize(tangent);
return new Vector4(tangent.x, tangent.y, tangent.z, -1);
}
根据以上思路,我们模拟平面Mesh构建过程,自定义顶点坐标,UV来计算顶点法线和切线来验证结果验证性,
代码如下
public class createPlane: MonoBehaviour
{
// Start is called before the first frame update
public Material mat;
public Texture2D tex;
int vertNum = 9;
int trangleNum = 8;
List<MyVert> vertList;
List<MyFace> faceList;
void Start()
{
create();
}
void create()
{
GameObject obj = new GameObject("plane");
MeshFilter mf = obj.AddComponent<MeshFilter>();
MeshRenderer mr = obj.AddComponent<MeshRenderer>();
Vector3[] vertices = new Vector3[vertNum];
Vector3[] normals = new Vector3[vertNum];
Vector4[] tangents = new Vector4[vertNum];
Vector2[] uvs = new Vector2[vertNum];
int[] triangles = new int[trangleNum * 3];
vertList = new List<MyVert>();
faceList = new List<MyFace>();
//set vert pos and uv
for (int i = 0;i < 3; ++i)
{
for(int j = 0;j < 3; ++j)
{
MyVert vert = new MyVert(i * 3 + j);
vert.pos = new Vector3(j * 1f, i, 0f);
vert.uv = new Vector2(j * 0.5f, i * 0.5f);
vertList.Add(vert);
}
}
//vertList[4].uv= new Vector2(0.25f, 0.75f);
//set trangle
int currentCount = 0;
triangles[currentCount++] = 0;
triangles[currentCount++] = 3;
triangles[currentCount++] = 4;
triangles[currentCount++] = 0;
triangles[currentCount++] = 4;
triangles[currentCount++] = 1;
triangles[currentCount++] = 1;
triangles[currentCount++] = 4;
triangles[currentCount++] = 5;
triangles[currentCount++] = 1;
triangles[currentCount++] = 5;
triangles[currentCount++] = 2;
triangles[currentCount++] = 3;
triangles[currentCount++] = 6;
triangles[currentCount++] = 7;
triangles[currentCount++] = 3;
triangles[currentCount++] = 7;
triangles[currentCount++] = 4;
triangles[currentCount++] = 4;
triangles[currentCount++] = 7;
triangles[currentCount++] = 8;
triangles[currentCount++] = 4;
triangles[currentCount++] = 8;
triangles[currentCount++] = 5;
//get trangle
for (int i = 0;i < trangleNum; i++)
{
MyVert[] verts = { vertList[triangles[i * 3]], vertList[triangles[i * 3 + 1]], vertList[triangles[i * 3 + 2]] };
MyFace face = new MyFace(i, verts);
face.Cal_Face_NT();
faceList.Add(face);
}
//get vert normal tangent
for(int i =0;i < vertNum;i++)
{
vertList[i].Cal_Face_NT(faceList);
vertices[i] = vertList[i].pos;
uvs[i] = vertList[i].uv;
normals[i] = vertList[i].normal;
tangents[i] = vertList[i].tangent;
}
mf.mesh.vertices = vertices;
mf.mesh.triangles = triangles;
mf.mesh.uv = uvs;
mf.mesh.normals = normals;
mf.mesh.tangents = tangents;
mr.material = new Material(Shader.Find("Standard"));
if (tex)
{
mr.material.SetTexture("_MainTex", tex);
}
obj.transform.position = new Vector3(0, 0, 0);
obj.transform.localScale = new Vector3(0.1f, 0.1f, 0.1f);
obj.transform.rotation = Quaternion.Euler(new Vector3(0, 0, 0));
obj.AddComponent<MeshTBN>();
}
}
结果如下图
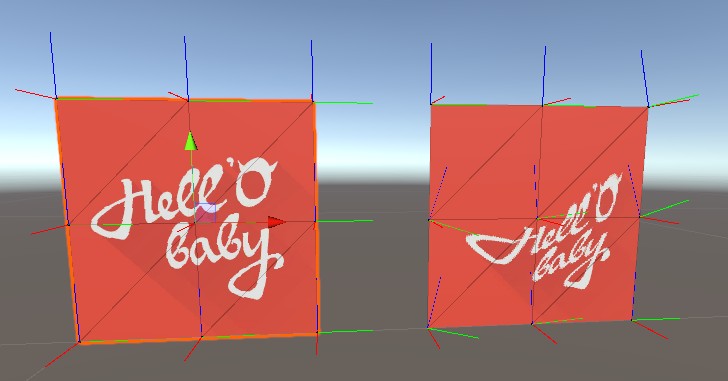
左边是初始的计算结果,右边是将中心点的uv调整后的计算结果,经过比对和Unity中的TBN计算结果一致
